Formal model of lemon senses

The primary model that we use to describe the semantics of lemon is inspired by this and views these tasks is that of an aligned semantic interpretation. Assume we have a language, $L$, on a vocabulary, $\Sigma$, i.e., $L \subseteq \Sigma^*$. Say we have a lexicon, $\mathcal{X}$, and we can define a language, $X \subseteq \mathcal{X}^*$, that constitutes all description of sentences in terms of the lexical entries it uses and the dependencies between the entries. Furthermore, we assume we have a lexicalization function $l$ that maps a sentence in the language to a list of lexical representations taken from a lexicon, $\mathcal{X}$, that is that $l$ is a function with the signature:

$$l : L \rightarrow X$$

We call such an $l$ a lexical interpretation and represents the result of the lexical parsing stages applied above, we simplify the definition here by assuming that this results in a single unambiguous representation relative to the lexicon.

Similarly assume we have an ontology $\mathcal{O}$, which can be used with a logic, $\mathcal{L}$, such that we have a language $O \subseteq (\mathcal{O} \cup \mathcal{L})^*$. Again, we define a function $s$ that maps a sentence in the language to its semantic representations, this function is called the semantic interpretation and has the signature:

$$s : L \rightarrow \mathcal{P}(O)$$

This function is indicated to input the set of correct results from all the lexical, correspondence and reasoning based analysis processes.

For example we take a simple sentence “The man bites the dog,” we assume that the lexicon contains the entities $\{ \mathrm{man}, \mathrm{dog}, \mathrm{bite(\cdot,\cdot)} \}$ and the ontology contains two classes $Man$ and $Dog$ and a property $bite$. Now, for example, we could have the folllowing interpretations:

$$l(\mathrm{“The\:man\:bites\:the\:dog”}) = \mathrm{bite(man,dog)}$$

$$s(\mathrm{“The\:man\:bites\:the\:dog”}) = \exists x,y : Man(x) \wedge Dog(y) \wedge bite(x,y)$$

We may then define an aligment, $A \subseteq (\mathcal{X} \times \mathcal{O})^*$ such that if we have $\mu \in X$, then for all $\sigma \in L$ such that $l(\sigma) = \mu$, we have $a_{\mu,p} \in A$ for each $p \in s(\sigma)$. Furthermore we require that if $\mu = \lambda_1\ldots\lambda_n$, $p =o_1\ldots o_m$ then we have $a_{\mu,p} = \alpha_1\ldots\alpha_n$ such that $\alpha_i = (\lambda_i,o_j)$ for some $j : 1 \leq j \leq m$.

We then define the set of senses in the lexicon, $S \subseteq (\mathcal{X}\times\mathcal{O})$, as the set satisfying

$$(\lambda,o) \in S \Leftrightarrow \exists \alpha_1\ldots\alp... ...rm{ such that } 1 \leq i \leq n \wedge \alpha_i = (\lambda,o)$$

As such our example may be explained by the following:

$$a_{\mu,p} = (\mathrm{bite(\cdot,\cdot)},bite) (\textrm{man},Man) (\textrm{dog},Dog)$$

$$\{ (\mathrm{man},Man) , (\mathrm{dog},Dog), (\mathrm{bite(\cdot,\cdot)},bite) \} \subseteq S$$

This can be illustrated as follows:

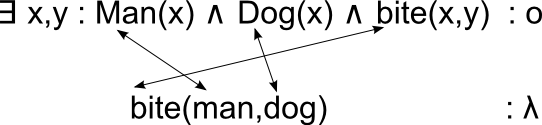
We view the sense as having three aspects:

• From the lexical point of view $s$ indicates a disambiguated usage of a term, we call this a Disambiguated Lexical Entry or DALE. We can formally define the set of DALEs, $D_{\lambda}$ for a lexical entry $\lambda$ as follows:
  
  $$D_{\lambda} = \{ d_{\lambda,o} \vert (\lambda,o) \in S \}$$
  
  

• From the semantic view, $s$ represents a sub-entity representing only the usage of a given class or property or individual when the given lexical entry is used to describe it. We call this an projected ontology sub-entity or POSE. We can formally define this as an ontology entity $\pi_s$ such that:
  
  $$\pi_s \sqsubseteq o$$
  
  
  
  
  $$\pi_s \equiv \bot \Leftrightarrow o \equiv \bot$$
  
  

• Finally we can view $S$ as a pair representing a possible alignment between the lexicographic and the semantic representations. We call this a correspondence.

We define the lemon senseRelations, equivalent, narrower, broader and incompatible and their relationship to the ontology as follows:

$$s_1 = s_2 \Leftrightarrow \pi_{s_1} \equiv \pi_{s_2}$$ (1)

$$s_1 < s_2 \Leftrightarrow \pi_{s_1} \sqsubset \pi_{s_2}$$ (2)

$$s_1 > s_2 \Leftrightarrow \pi_{s_1} \sqsupset \pi_{s_2}$$ (3)

$$s_1 \otimes s_2 \Leftrightarrow \pi_{s_1} \sqcap \pi_{s_2} = \bot$$ (4)

Theorem

If we have $o_1,o_2 \in \mathcal{O}$ and some corresponding senses $s_1,s_2 \in S$ then the following hold:

1. $o_1 \sqcap o_2 \equiv \bot \vdash s_1 \otimes s_2$
2. $s_1 = s_2 \vdash o_1 \sqcap o_2 \not\equiv \bot \vee o_2 \equiv o_1 \equiv \bot$
3. $s_1 > s_2 \vdash o_1 \sqcap o_2 \not\equiv \bot \vee o_2 \equiv \bot$

Proof

1. We have $\pi_{s_1} \sqsubseteq o_1$ and $\pi_{s_2} \sqsubseteq o_2$ hence $\pi_{s_1} \sqcap \pi_{s_2} \sqsubseteq o_1 \sqcap o_2$ hence we have $\pi_{s_1} \sqcap \pi_{s_2} \equiv \bot$ hence $s_1 \otimes s_2$
2. Assume $o_2 \not\equiv \bot$ hence it follows that $\pi_{s_2} \not\equiv\bot$, but we have $\pi_{s_2} \equiv \pi_{s_1}$ hence $o_1 \sqcap o_2 \sqsupseteq \pi_{s_1} \sqcap \pi_{s_2} \equiv \pi_{s_2} \not\equiv \bot$. Similarly for $o_1 \not\equiv \bot$.
3. (As 2.)

As a motivating example for making this distinction consider the example of “student” and “person”, these are asserted to be hypernyms in WordNet however in a strict ontology sense are not in a subsumption (subclass) relation. In fact “student” is a role of a “person” and would not be modeled the same in a well-reasoned ontology (i.e., DOLCE, which would distinguish “student” as anti-rigid and “person” as rigid). However for certain tasks, such as coreference resolution, it is necessary to have these “lexical” semantics, and as such we include them within the lexicon. As such it is possible to state the “student“ is a narrower sense of “person”, without affecting the correctness or the ontology.

In the context of coreference this modelling can be used for word sense disambiguation and coreference as it contains lexical semantics that are weaker than those in the ontology. In particular, there are four relations defined in lemon that are used to aid these tasks: equivalent, disjoint, broader and narrower. Each of these can be understood in the following manner.

• equivalent: Two DALEs which have equivalent senses can be substituted for each other without changing the semantics of the text. This should be assumed to be a positive feature for coreference.
• incompatible: Two DALEs which have incompatible (disjoint) senses cannot be substituted for each other without changing the semantics of the text. This should be considered to be a negative feature for coreference.
• broader/narrower: If a DALE is asserted to be broader than another DALE, then it can be substituted to give a more general semantics. This should be considered a positive feature for coreference, if the preceding term is narrower.